Numpy เบื้องต้น - 2 D
Contents

Numpy เบื้องต้น - 2 D#
20 minutes
วัตถุประสงค์
หลังจากทำทำแล็บ นศ.จะสามารถ
สร้างและดำเนินการทางคณิตศาสตร์กับข้อมูลชนิด
numpyอาร์เรย์ 2 มิติได้
Ref:
ความสำคัญของข้อมูลอาร์เรย์ สถิติ หลายมิติ RBG …
การสร้างอาร์เรย์ 2 มิติ (2D Numpy Array)#
# Import the libraries
import numpy as np
import matplotlib.pyplot as plt
สร้างลิสต์ (List) a ขึ้นมา ซึ่งเป็น nested list 3 ลิสต์ที่มีขนาดเท่ากัน
# Create a list
#a = [[11, 12, 13], [21, 22, 23], [31, 32, 33]]
a = [[11, 12, 13],
[21, 22, 23],
[31, 32, 33]]
a
[[11, 12, 13], [21, 22, 23], [31, 32, 33]]
เราสามารถสร้าง Numpy Array จากลิสต์ได้ ดังต่อไปนี้
# Convert list to Numpy Array
# Every element is the same type
A = np.array(a)
A
array([[11, 12, 13],
[21, 22, 23],
[31, 32, 33]])
เราสามารถเรียกแอตทริบิวต์ (attribute) ndim (number of dimensions) เพื่อดูจำนวนแกน (axes) หรือ จำนวนมิติ (dimensions) ของอาเรย์ได้
# Show the numpy array dimensions
A.ndim
2
แอตทริบิวต์ shape ส่งค่ากลับเป็นข้อมูลชนิด tuple ที่สอดคล้องกับขนาด (size) หรือจำนวนสมาชิกในแต่ละมิติ (รูปร่างของอาเรย์)
# Show the numpy array shape
A.shape
(3, 3)
จำนวนสมาชิกทั้งหมดที่มีอยู่ในอาร์เรย์สามารถดูได้จากแอตทริบิวต์ size.
# Show the numpy array size
A.size
9
การเข้าถึงสมาชิกในอาร์เรย์#
เช่นเดียวกันกับอาร์เรย์ 1 มิติ เราสามารถเข้าถึงข้อมูลแต่ละตัวภายในอาร์เรย์ได้โดยใช้เครื่องหมายวงเล็บเหลี่ยม (ก้ามปู) [ ] (square brackets)
ความสัมพันธ์ระหว่างเลขดัชนีในวงเล็บเหลี่ยมกับสมาชิกแต่ละตัวแสดงได้ในรูปต่อไปนี้ (อาร์เรย์ 3x3)
อาร์เรย์ 2 มิติ คือ Array of Array

เราสามารถเข้าถึงสมาชิกที่อยู่ในแถวที่ 2 (2nd-row) และคอลัมน์ที่ 3 (3rd column) ดังแสดงในรูป
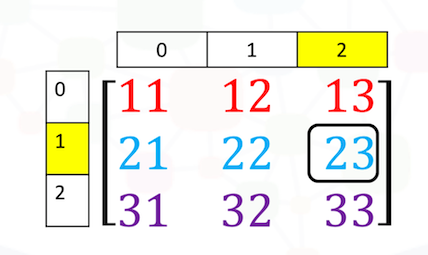
โดยใช้เครื่องหมายวงเล็บเหลี่ยม [ ] และดัชนีที่สอดคล้องกับตำแน่งที่เราต้องการ
# Access the element on the second row and third column
A[1, 2]
23
หรือจะเขียนรูปแบบแบบนี้ก็ได้ ให้ผลลัพธ์เหมือนกัน (มีสองรูปแบบ!)
# Access the element on the second row and third column
A[1][2]
23
ลองเข้าถึงสมาชิกที่กำหนดในรูปภาพต่อไปนี้
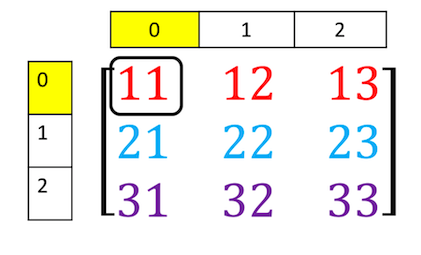
แถวที่ 0 คอลัมน์ที่ 0 ดังนั้น
# Access the element on the first row and first column
A[0][0]
11
เราสามารถตัดเฉพาะส่วน (slicing) ได้เช่นเดียวกัยอาร์เรย์ 1 มิติ
รูปด้านล่าง: เราจะตัดเอาเฉพาะสองคอลัมน์แรกที่อยู่ในแถวแรกเท่านั้น
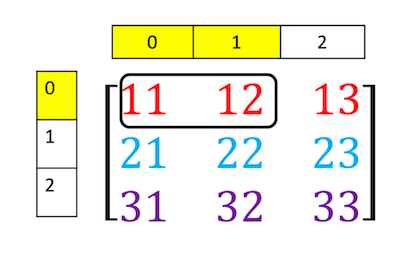
ตัดได้โดยใช้คำสั่งต่อไปนี้
# Access the element on the first row and first and second columns
A[0][0:2]
array([11, 12])
เช่นเดียวกัน เราสามารถตัดเอาเฉพาะสองแถวแรกที่อยู่ในคอลัมน์ที่ 3 เท่านั้น
# Access the element on the first and second rows and third column
A[0:2, 2]
array([13, 23])
ดังแสดงในรูป
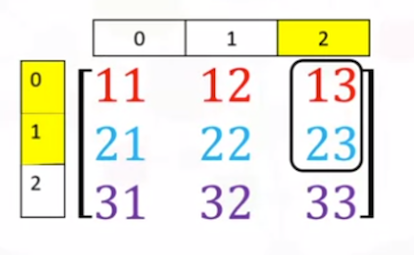
สมาชิกที่อยู่ในแถวที่ 0, แถวที่ 1, แถวที่ 2 ตามลำดับ
A[0]
array([11, 12, 13])
A[1]
array([21, 22, 23])
A[2]
array([31, 32, 33])
หรือแบบนี้ก็ได้
A[2, :]
array([31, 32, 33])
สมาชิกที่อยู่ในคอลัมน์ที่ 0, คอลัมน์ที่ 1, คอลัมน์ที่ 2 ตามลำดับ
A[:][0]
array([11, 12, 13])
A[:][1]
array([21, 22, 23])
A[:][2]
array([31, 32, 33])
การดำเนินการสำหรับ Numpy Array 2 มิติขั้นพื้นฐาน#
เรายังสามารถบวกอาร์เรย์ได้อีกด้วย การบวกนี้เหมือนกับการบวกเมทริกซ์ กล่าวคือเป็นการนำสมาชิกแต่ละตัวมาบวกกันเป็นคู่ๆ
รูปต่อไปนี้แสดงการบวกเมทริกซ์ X และ Y
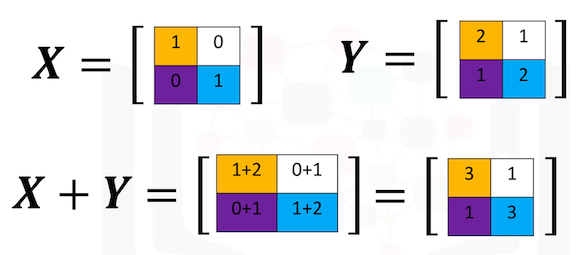
สร้างอาร์เรย์ X และ Y ขึ้นมา
# Create a numpy array X
X = np.array([[1, 0], [0, 1]])
X
array([[1, 0],
[0, 1]])
# Create a numpy array Y
Y = np.array([[2, 1], [1, 2]])
Y
array([[2, 1],
[1, 2]])
ทำการบวกอาร์เรย์ X และ Y ด้วยคำสั่งต่อไปนี้
# Add X and Y
Z = X + Y
Z
array([[3, 1],
[1, 3]])
ทำการลบอาร์เรย์ X และ Y ด้วยคำสั่งต่อไปนี้
# X - Y
Z = X - Y
Z
array([[-1, -1],
[-1, -1]])
อาร์เรย์จะบวกลบกันได้ ก็ต่อเมื่อมีรูปร่าง (shape) เหมือนกัน!
X = np.array([[1, 0, 1], [0, 1, 1]])
Y = np.array([[2, 1], [1, 2], [1, 1]])
print(X)
print(Y)
[[1 0 1]
[0 1 1]]
[[2 1]
[1 2]
[1 1]]
# ValueError: operands could not be broadcast together with shapes (2,3) (3,2)
#Z = X+Y
#print(Z)
การคูณ Numpy array ด้วยสเกลาร์นั้นเหมือนกับการคูณเมทริกซ์ด้วยสเกลาร์ ถ้าเราคูณเมทริกซ์ Y ด้วยสเกล 2 เราก็คูณทุกองค์ประกอบในเมทริกซ์ด้วย 2 ดังที่แสดงในรูป
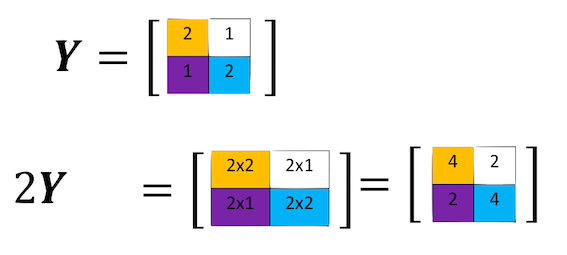
คูณอาร์เรย์ Y ด้วย 2
# Create a numpy array Y
Y = np.array([[2, 1], [1, 2]])
Y
array([[2, 1],
[1, 2]])
# Multiply Y with 2
Z = 2 * Y
Z
array([[4, 2],
[2, 4]])
การคูณอาร์เรย์สองอาร์เรย์เป็น การคูณฮาดามาร์ด (Hadamard product/Element-wise multiplication) *
การคูณ Hadamard เป็นการคูณแต่ละสมาชิกที่อยู่ในตำแหน่งเดียวกันเป็นคู่ๆ ผลลัพธ์ของการคูณจะมีขนาดเดียวกับ X หรือ Y ดังแสดงในรูปต่อไปนี้
* ผลคูณฮาดามาร์ดใช้ในการวิเคราะห์เชิงสถิติ โดยเฉพาะอย่างยิ่งใช้ในแบบจำลองเชิงเส้นทั่วไป (general linear models) และแบบจำลองการวิเคราะห์ตัวประกอบในรูปทั่วไป (generalized factor analysis model)
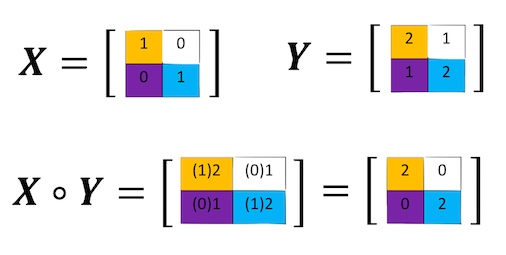
เราสามารถคูณแต่ละสมาชิกของอาร์เรย์ X และ Y ได้โดยการเขียนโค้ดต่อไปนี้
# Create a numpy array X
X = np.array([[1, 0], [0, 1]])
X
array([[1, 0],
[0, 1]])
# Create a numpy array
Y = np.array([[2, 1], [1, 2]])
Y
array([[2, 1],
[1, 2]])
# Multiply X with Y
Z = X * Y
Z
array([[2, 0],
[0, 2]])
นอกจากการคูณแล้ว การหาร การยกกำลัง และหารเอาเศษ ก็เป็นการคำนวณเป็นคู่ๆ ทีละตัว ดังตัวอย่างต่อไปนี้
print(X/Y, '\n')
print(X**Y, '\n')
print(X%Y, '\n')
[[0.5 0. ]
[0. 0.5]]
[[1 0]
[0 1]]
[[1 0]
[0 1]]
คูณแบบเมทริกซ์
นอกจากนี้ เรายังสามารถคูณ Numpy arrays A และ B แบบเมทริกซ์ ได้อีกด้วย
ก่อนอื่น กำหนดเมทริกซ์ A (2x3) และ B (3x2)
# Create a matrix A
A = np.array([[0, 1, 1], [1, 0, 1]])
A
array([[0, 1, 1],
[1, 0, 1]])
# Create a matrix B
B = np.array([[1, 1], [1, 1], [-1, 1]])
B
array([[ 1, 1],
[ 1, 1],
[-1, 1]])
ใช้ฟังก์ชั่น dot คูณอาร์เรย์ทั้งสอง
# Calculate the dot product
Z = np.dot(A,B)
Z
array([[0, 2],
[0, 2]])
# Calculate the sine of Z
np.sin(Z)
array([[0. , 0.90929743],
[0. , 0.90929743]])
เราสามารถเรียกแอตทริบิวต์ T (Transpose) เพื่อคำนวณเมทริกซ์สลับเปลี่ยน (Transpose) สลับแถวและคอลัมน์
Note: เมทริกซ์สลับเปลี่ยน (transpose of a matrix) คือเมทริกซ์ที่ได้จากการสลับสมาชิกจากแถวเป็นคอลัมน์ และจากคอลัมน์เป็นแถวของเมทริกซ์ต้นแบบ เมตริกซ์ทรานสโพสของ A เขียนแทนด้วย AT
# Create a matrix C
C = np.array([[1,1],[2,2],[3,3]])
C
array([[1, 1],
[2, 2],
[3, 3]])
# Get the transposed of C
C.T
array([[1, 2, 3],
[1, 2, 3]])
C.T.T
array([[1, 1],
[2, 2],
[3, 3]])
[Exercise]#
1 จงเขียนโค้ดเปลี่ยนลิสต์ a ต่อไปนี้ให้เป็น Numpy Array
# Write your code below and press Shift+Enter to execute
a = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]
Click here for the solution
A = np.array(a)
A
2 จงคำนวณหาจำนวนสมาชิกหรือขนาด (size) ของอาร์เรย์
# Write your code below and press Shift+Enter to execute
Click here for the solution
A.size
3 จงเข้าถึงสมาชิกที่อยู่ในแถวแรกคอลัมน์แรก และ แถวแรกคอลัมน์ที่สอง
# Write your code below and press Shift+Enter to execute
Click here for the solution
A[0][0:2]
4 จงหาผลคูณแบบเมทริกซ์ของ numpy arrays A และ B
# Write your code below and press Shift+Enter to execute
B = np.array([[0, 1], [1, 0], [1, 1], [-1, 0]])
Click here for the solution
X = np.dot(A,B)
X
Change Log#
Date |
Version |
Change Description |
|---|---|---|
08-08-2021 |
0.1 |
First edition |